15.2 偏微分方程

ReacTran 的几个关键函数介绍

一维热传导方程

$$\{\begin{array}{l}\frac{\mathrm{\partial }y}{\mathrm{\partial }t}=D\frac{{\mathrm{\partial }}^{2}y}{\mathrm{\partial }{x}^2}\end{array}$$

参数 $D=0.01$，边界条件 $y_{t,x=0}=0,y_{t,x=1}=1$，初始条件 $y_{t=0,x}=\sin (\pi x)$。

library(ReacTran)

N <- 100
xgrid <- setup.grid.1D(x.up = 0, x.down = 1, N = N)
x <- xgrid$x.mid
D.coeff <- 0.01
Diffusion <- function(t, Y, parms) {
  tran <- tran.1D(
    C = Y, C.up = 0, C.down = 1,
    D = D.coeff, dx = xgrid
  )
  list(
    dY = tran$dC, 
    flux.up = tran$flux.up,
    flux.down = tran$flux.down
  )
}
yini <- sin(pi * x)
times <- seq(from = 0, to = 5, by = 0.01)
out <- ode.1D(
  y = yini, times = times, func = Diffusion,
  parms = NULL, dimens = N
)

image(out,
  grid = xgrid$x.mid, xlab = "times",
  ylab = "Distance", main = "PDE", add.contour = TRUE
)

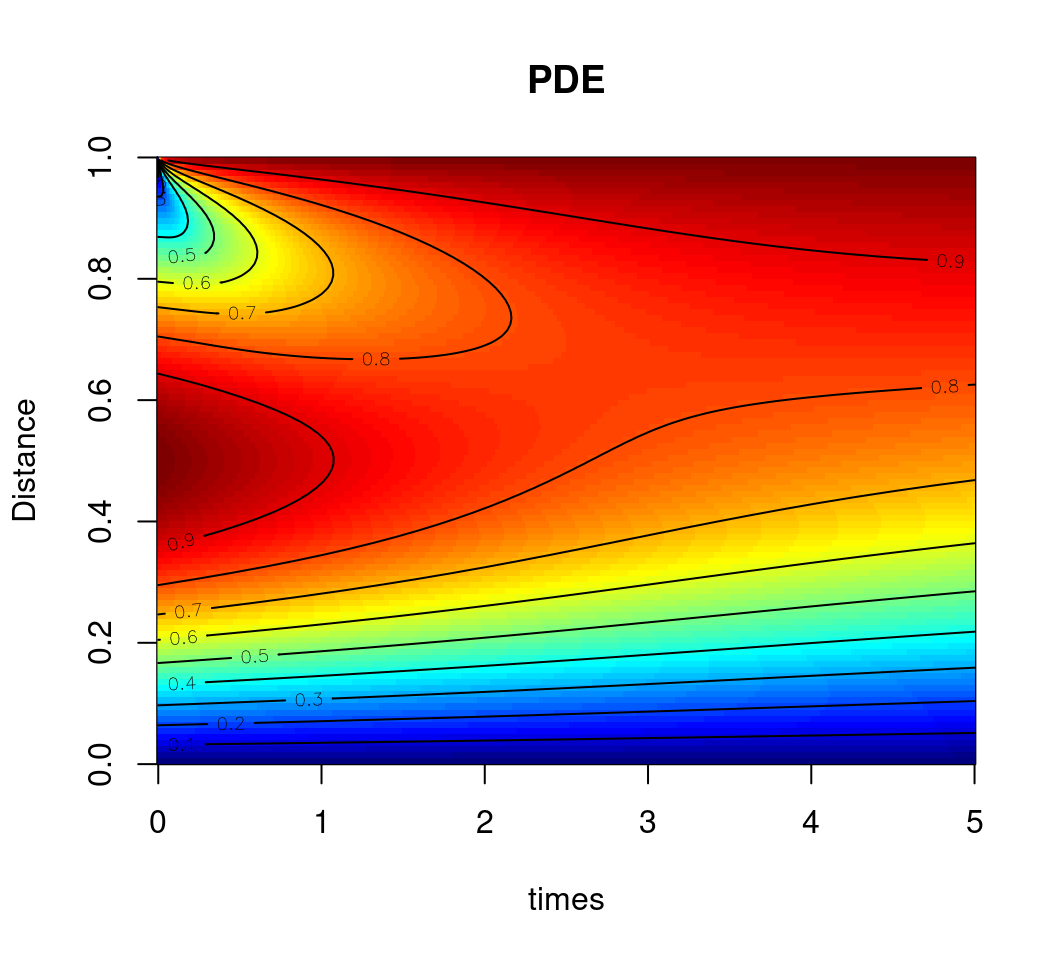
图 15.2: 一维热传导方程的数值解热力图

二维拉普拉斯方程

$$\{\begin{array}{l}\frac{{\mathrm{\partial }}^{2}u}{{\mathrm{\partial }}^{2}x}+\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}=0\end{array}$$

边界条件

$$\{\begin{array}{l}{u}_{x=0,y}=u_{x=1,y}=0\\ \frac{\mathrm{\partial }{u}_{x,y=0}}{\mathrm{\partial }y}=0\\ \frac{\mathrm{\partial }{u}_{x,y=1}}{\mathrm{\partial }y}=\pi \sinh (\pi )\sin (\pi x)\end{array}$$

它有解析解

$$u(x,y)=\sin (\pi x)\cosh (\pi y)$$

其中 $x\in [0,1],y\in [0,1]$

fn <- function(x, y) {
  sin(pi * x) * cosh(pi * y)
}
x <- seq(0, 1, length.out = 101)
y <- seq(0, 1, length.out = 101)
z <- outer(x, y, fn)

image(z, col = terrain.colors(20))
contour(z, method = "flattest", add = TRUE, lty = 1)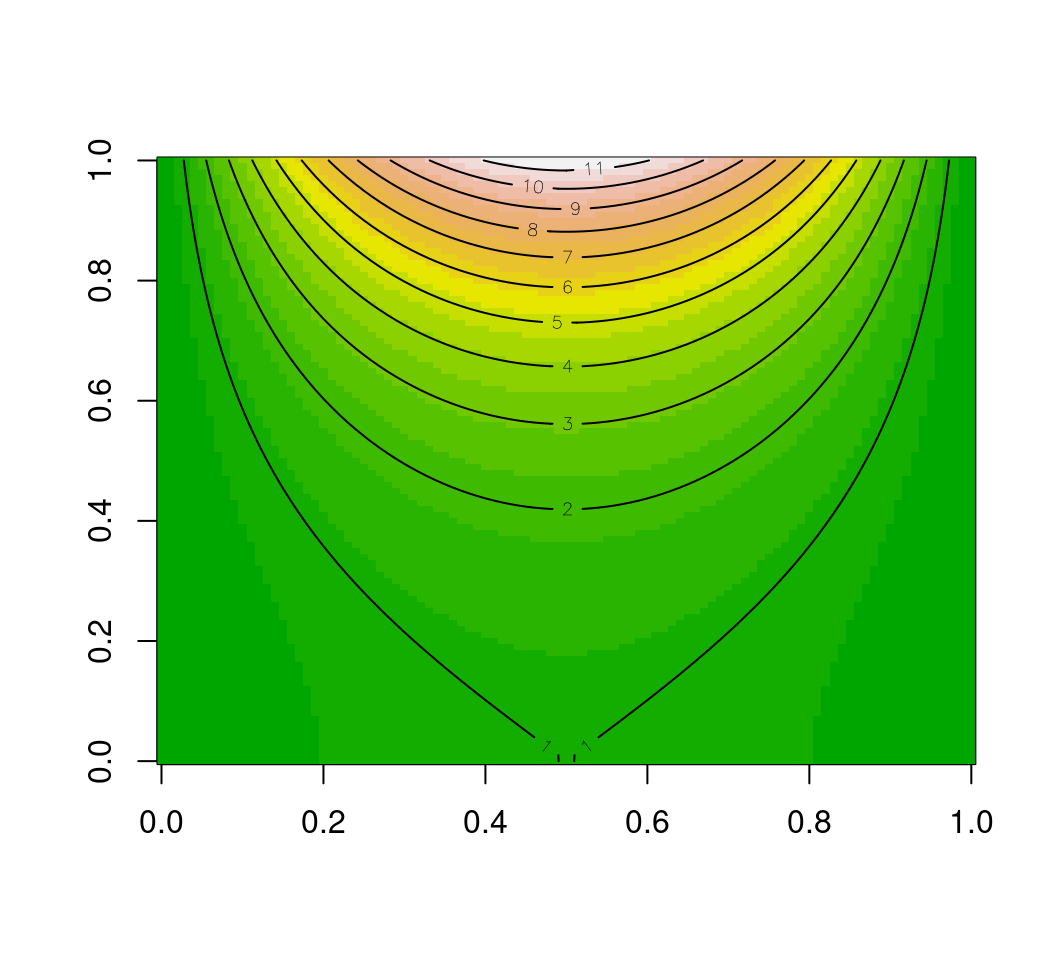

图 15.3: 解析解的二维图像

persp(z, 
  theta = 30, phi = 20, 
  r = 50, d = 0.1, expand = 0.5, ltheta = 90, lphi = 180,
  shade = 0.1, ticktype = "detailed", nticks = 5, box = TRUE,
  col = drapecol(z, col = terrain.colors(20)),
  border = "transparent",
  xlab = "X", ylab = "Y", zlab = "Z", 
  main = ""
)

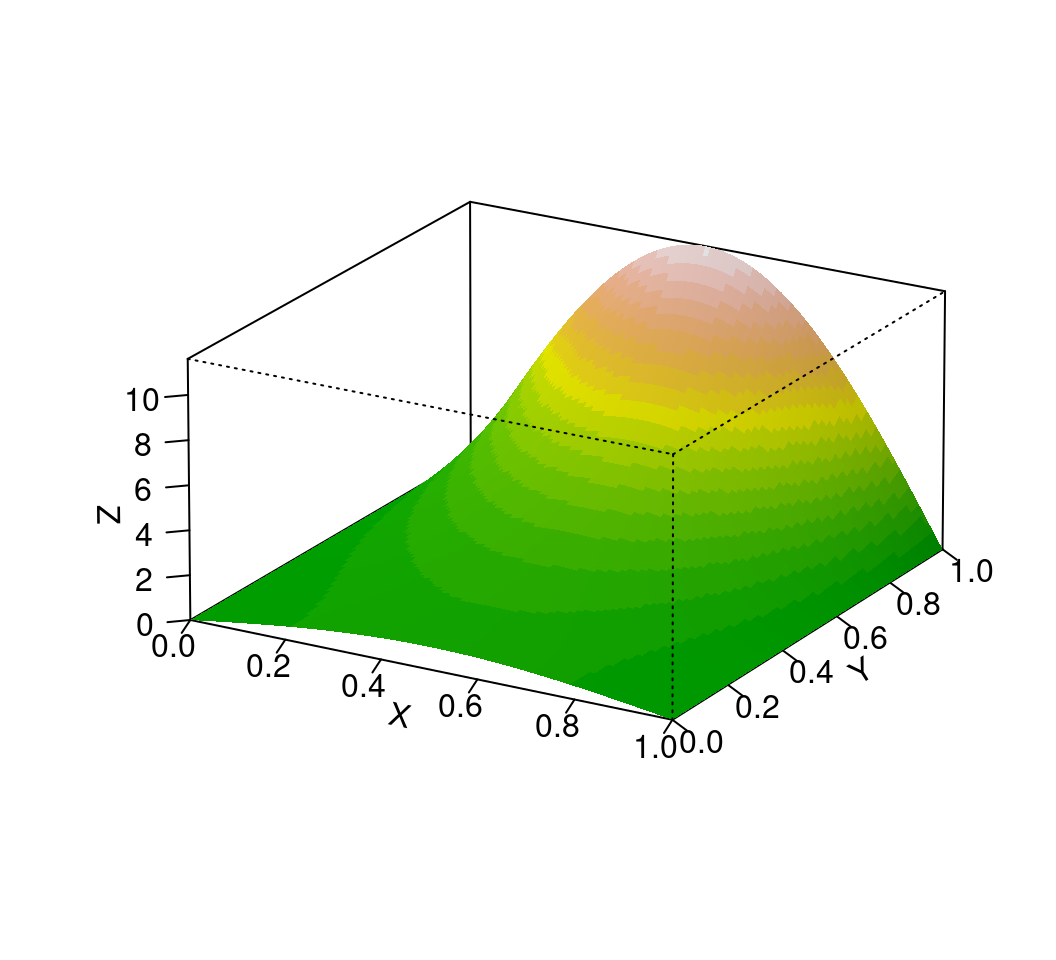
图 15.4: 解析解的三维透视图像

求解 PDE

dx <- 0.2
xgrid <- setup.grid.1D(-100, 100, dx.1 = dx)
x <- xgrid$x.mid
N <- xgrid$N

uini <- exp(-0.05 * x^2)
vini <- rep(0, N)
yini <- c(uini, vini)
times <- seq(from = 0, to = 50, by = 1)

wave <- function(t, y, parms) {
  u1 <- y[1:N]
  u2 <- y[-(1:N)]
  du1 <- u2
  du2 <- tran.1D(C = u1, C.up = 0, C.down = 0, D = 1, dx = xgrid)$dC
  return(list(c(du1, du2)))
}

out <- ode.1D(
  func = wave, y = yini, times = times, parms = NULL,
  nspec = 2, method = "ode45", dimens = N, names = c("u", "v")
)